Le considerazioni che seguono si riferiscono all’applicazione delle norme tecniche del DM Infrastrutture 17/01/2018 (in seguito indicate come NTC 2018) relative ai pali in gruppo così come implementate nel programma Fondazioni CA di GeoStru .
Una prima importante distinzione da fare è quella tra pali isolati e pali in gruppo. Possono considerarsi pali isolati quelli disposti in modo che la loro distanza reciproca superi 6÷8 volte il loro diametro (ad esempio pali che portano singolarmente i pilastri e siano collegati da un graticcio di travi o da una platea). I pali che invece sono più vicini della suddetta distanza (detta di estinzione) e che siano tra loro collegati da un unica testata vanno considerati come pali in gruppo (ad esempio ogni plinto su più pali realizza un gruppo; come pure una platea su pali ravvicinati).
Per evitare eccessive interazioni e quindi eccessivi cedimenti i pali non devono mai essere a distanza reciproca minore di 3 volte il loro diametro.
Per i pali isolati la resistenza caratteristica, di tipo GEO, assiale e trasversale va calcolata con riferimento ad ognuno di essi, dividendo le resistenze ultime per i fattori di correlazione (§ 6.4.3.1.1, § 6.4.3.1.2 NTC). Calcolate così le resistenze caratteristiche queste vanno a loro volta divise per i coefficienti parziali R3 per ottenere le resistenze di progetto con cui verificare singolarmente i pali. Anche i cedimenti assoluti dei pali vanno verificati palo per palo controllando, inoltre, eventuali cedimenti e rotazioni differenziali.
Per i pali in gruppo le NTC 2018 fanno una precisa distinzione tra il calcolo di resistenza GEO per gli stati limite ultimi SLU e quello degli stati limite di esercizio SLE, quest’ultimo orientato prevalentemente al calcolo degli spostamenti e distorsioni. Mentre per il primo tipo di calcolo (SLU/SLV) viene richiesto di tener conto delle possibili riduzioni di resistenza dei pali per effetto di gruppo, per il secondo oltre all’effetto di gruppo si chiede di tenere sopratutto conto degli effetti di interazione tra i pali. Mettere in conto l’effetto di gruppo (sia nelle verifiche SLU che in quelle SLE) consiste in pratica nel valutare (caso per caso) due fattori di efficienza (uno per forze assiale, l’altro per forze trasversali) mediante i quali ridurre la somma delle resistenze complessive dei pali.
Mettere in conto, nelle verifiche SLE, gli effetti di interazione (essenzialmente quelli assiali per carichi verticali) significa invece valutare con maggiore attenzione i maggiori cedimenti e distorsioni che tali effetti vanno a produrre sia nella struttura di fondazione che nella sovrastruttura.
Poiché nel programma ‘Fondazioni in ca’ è stata prevista una valutazione specifica dell’interazione assiale tra i pali basata sul metodo dei coefficienti di influenza si consiglia di effettuare due distinti calcoli della stessa struttura di fondazione in presenza di pali in gruppo:
1) Un primo calcolo contenente le sole combinazioni SLU con la definizione dei fattori di efficienza per effetti di gruppo senza mettere in conto l’interazione assiale tra i pali.
2) Un secondo calcolo contenente le sole combinazioni SLE in cui oltre ai fattori di efficienza per effetti di gruppo si consideri l’interazione assiale tra i pali.
Le armature finali del progetto risulteranno dall’inviluppo di quelle verificate in entrambi i calcoli.
Si consiglia questa metodologia di calcolo anche nel caso di fondazioni miste (qui non considerate ma previste nel programma).
La verifica geotecnica (GEO) dei pali deve tenere conto dell’effetto di gruppo sia nelle combinazioni SLU che nelle combinazioni SLE (§ 6.4.3 NTC). A tale scopo viene utilizzato un fattore di efficienza Eg tale da ridurre la somma delle resistenze assiali degli n pali in gruppo: Rgruppo = Eg·n·Rsingolo.
La scelta del valore di Egruppo dipende dal numero di pali, dalla geometria del gruppo etc..
Nel caso di terreni incoerenti Egruppo va posto pari ad 1.00.
Analogo coefficiente empirico Ggruppo di efficienza va stimato nella verifica a collasso per carichi trasversali sia per terreni coesivi che per terreni incoerenti. E’ sempre possibile trascurare la portanza superficiale della struttura di collegamento dei pali (platea, travi, plinti). Nel caso in cui, però, la si voglia considerare è necessario svolgere un’apposita analisi di interazione geotecnica tra pali e struttura di collegamento (il calcolo delle fondazioni miste è previsto in programma mediante l’impiego di uno specifico algoritmo).
Una norma innovativa introdotta dalle NTC 2018 è contenuta nel § 6.4.3.1.1.1:
“Per una palificata, la verifica della condizione [6.2.1] dovrà essere fatta in base alla resistenza caratteristica che risulta dalla somma delle resistenze caratteristiche dei pali che la costituiscono. Sarà comunque necessario valutare possibili riduzioni della resistenza disponibile per effetto di gruppo, tenendo conto della tipologia dei pali, della natura dei terreni interessati e della configurazione geometrica della palificata”.
Quindi per pali in gruppo distanti tra loro meno di 6 volte il diametro non andrebbe più verificata la resistenza assiale di progetto di ogni palo bensì quella caratteristica somma delle resistenze caratteristiche di tutti i pali del gruppo.
Ad avviso di chi scrive l’applicazione di questa norma dovrebbe essere fatta prevedendo un calcolo dei pali assialmente non lineare (la resistenza non deve poter superare quella limite di ogni palo). Di conseguenza (ed in via prudenziale) in presenza di pali in gruppo (plinti su pali predefiniti e pali tra loro a distanza minore di 6 volte il loro diametro ed indicati nei Dati Generali con il fattore di efficienza Ev<1), il programma continua ad effettuare la verifica di resistenza assiale di singolo ogni palo del gruppo, ma lo fa confrontando la forza assiale di combinazione agente sul palo con la resistenza caratteristica e non con la resistenza di progetto (come precedentemente previsto). Per operare questa innovativa verifica basta assegnare come resistenza assiale di progetto quella caratteristica.
Le resistenze di progetto dei pali possono essere calcolate sia a partire da formulazioni analitiche basate sui parametri geotecnici da prove in sito, sia da prove dirette di carico su pali pilota. Per quanto riguarda le verifiche SLE vanno anzitutto assegnati i cedimenti e spostamenti trasversali limite dipendenti dai requisiti prestazionali dell’opera in elevazione. I massimi cedimenti differenziali e le distorsioni rotazionali vanno calcolati a partire dai cedimenti e rotazioni assoluti forniti dal calcolo.
La normativa sismica (§ 7.11.2 NTC 2018) richiede in astratto che la caratterizzazione geotecnica in cui sia valutata la dipendenza della rigidezza e dello smorzamento dal livello deformativo E’ inoltre necessaria una valutazione dell’interazione reciproca tra i pali in gruppo (§ 6.4.3 NTC) sottoposti, nel caso sismico, a forze orizzontali dinamiche e cinematiche.
Il calcolo dei pali in gruppo sottoposti ad azioni dinamiche di tipo sismico rappresenta uno dei capitoli più complessi ed ancora non del tutto esplorati dell’analisi strutturale. Ricerche sono ancora in corso per validare metodologie di calcolo semplificate che evitino il ricorso a metodi generali di soluzione che dovrebbero analizzare la palificata mediante un’analisi dinamica non lineare al passo sotto un accelerogramma di progetto tenendo conto degli effetti dinamici di gruppo, della degradazione ciclica e dell’interazione sia con un terreno stratificato che con la struttura in elevazione.
A causa della forte non linearità delle reazioni orizzontali del terreno lungo i pali, l’analisi modale in quanto lineare non è molto coerente con le suddette ipotesi. Come pure discutibile risulta l’uso delle impedenze (rigidezze funzione della frequenza espresse mediante numeri in campo complesso) in sostituzione delle rigidezze alla traslazione dei pali.
Una prima semplificazione del problema viene dal § 7.2.6 delle NTC quando a proposito della valutazione dell’interazione dinamica tra fondazione e terreno afferma che è “possibile” (non obbligatorio) “tenere conto della modifica del moto sismico indotta dall’interazione fondazione-terreno” mediante vincoli visco elastici (impedenze dinamiche che tengano conto del livello deformativo….).
Per opere di non primaria importanza e complessità possono, quindi, essere impiegati metodi di calcolo semplificati pseudo-statici che, come sopra specificato, prevedano anche un comportamento non lineare del terreno in cui sono immersi i pali ed anche una valutazione diretta dell’interazione tra i pali.
Assunta quest’ultima ipotesi semplificativa, si descrivono di seguito le ipotesi assunte per il calcolo dei pali in gruppo a partire da quelle relative al palo singolo.
Il calcolo degli spostamenti e delle sollecitazioni del palo singolo va effettuato considerando la sezione di estremità superiore del palo connessa alle travi o alla piastra di collegamento con vincolo di continuità o di cerniera sferica. Nel caso generale si possono calcolare pali in gruppo collegati tra loro a mezzo di una trave, di un graticcio di travi, di una platea di forma qualsiasi semplice o nervata. L’interazione tra i pali e la struttura di collegamento orizzontale (testata) avviene unicamente in corrispondenza dei nodi principali in cui sono applicati i pali. In ogni nodo principale i gradi di libertà attivi sono costituiti, pertanto, dalle solite tre componenti di movimento considerate nel calcolo dei graticci e/o delle piastre (lo spostamento verticale e dalle due rotazioni intorno alla direzione degli assi X,Y del riferimento generale). A questi vanno aggiunte le tre componenti di movimento nel piano orizzontale, molto spesso uniche per tutti i nodi (spostamenti in direzione X,Y e rotazione intorno all’asse Z), con ciò trascurando le deformazioni assiali nel piano orizzontale X,Y in quanto sicuramente ininfluenti a causa delle massicce dimensioni usualmente impiegate per le strutture orizzontali di collegamento dei pali. In generale, quindi, per poter assemblare nella matrice di rigidezza globale della struttura il singolo palo occorre costruire una matrice di rigidezza del palo che tenga conto dei sei gradi di libertà attivi in corrispondenza del nodo di innesto del palo nella testata.
Pali nel modello di Winkler con terreno a comportamento lineare
Ogni palo viene considerato dal programma come una sotto-struttura elastica da assemblare nel sistema risolvente generale dell’intera struttura (metodo delle deformazioni) mediante i valori delle rigidezze del nodo di testa (matrice rigidezze 6×6 corrispondente ai 6 gradi di libertà della testa del palo). Ogni palo viene discretizzato in elementi beam nei cui nodi di estremità sono applicate molle lineari trasversali che rappresentano la reazione elastica del terreno ad ogni spostamento trasversale dei nodi delle beam. Dette molle possono assumere rigidezza variabile lungo il fusto in base ai parametri geotecnici assegnati alla tipologia di palo a cui il palo appartiene.
Per i pali in gruppo e nel caso di combinazioni di esercizio SLE può essere messa in conto l’interazione assiale tra i pali implementata col metodo dei coefficienti di influenza.
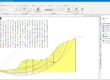
Nel modello di palo con terreno a comportamento lineare la rigidezza assiale per carico concentrato applicato sulla testa del palo viene determinata con riferimento al grafico di seguito riportato che illustra la relazione di Randolph-Wroth-Fleming (1992):


In cui:
η = db / d si assume qui db = d e quindi η = 1
ξ = GL/ Gb si assume qui Gb=GL e quindi ξ = 1
ρ = Gavg / GL
λ = Ep /GL con Ep modulo elastico del palo
rm = [0.25 + (0.25 ρ (1-ν) – 0.25) ξ ] L distanza di estinzione dell’interazione tra pali (detto ‘raggio magico’)
ς = ln(2 rm /d)
μL = 2 (2/(ςλ))0.5 (L/d)
Per applicare le suddette relazioni nel caso di terreno stratificato il valore Gavg viene calcolato come media ponderale dei valori del modulo elastico G lungo il fusto del palo.
Ogni palo viene discretizzato in conci di trave (elementi beam) aventi lunghezza pari alla mesh assegnata. In ogni nodo di estremità dei conci viene applicata una molla lineare o non lineare che rappresenta la reazione trasversale del terreno lungo le due metà dei conci a cavallo del nodo.
Pali nel modello di Winkler con terreno a comportamento non lineare (Curve di trasferimento p-y, t-z)
In presenza di significative forze orizzontali (in combinazioni SLU/SLV) agenti sui pali la reazione trasversale del terreno sui pali è spiccatamente non lineare per cui l’impiego delle molle lineari per modellare detta reazione del terreno diventa solo una rozza approssimazione (gli sforzi sui pali aumentano più che proporzionalmente all’aumentare delle forze orizzontali).
Di conseguenza si consiglia di utilizzare questo modello di terreno non lineare per meglio valutare spostamenti trasversali e sollecitazioni nei pali in presenza di forti forze trasversali agenti sui pali.
Nel calcolo non lineare una volta risolto il sistema generale (i pali e le altre strutture di fondazione restano sempre a comportamento elastico lineare), vengono aggiornate tutte le rigidezze delle molle non lineari rappresentative del terreno in funzione degli spostamenti ottenuti dalla risoluzione del sistema generale.
Il sistema generale viene quindi riassemblato e risolto ottenendo nuovi spostamenti per i nodi di testa dei pali (ed anche nuove sollecitazioni nei pali e nelle testate dei pali). Il procedimento viene iterato fino a che tutti gli spostamenti risultino pressoché uguali a quelli dell’iterazione precedente. L’espressione analitica non lineare della reazione del terreno viene denominata in letteratura come curva di trasferimento p-y in cui p è la pressione del terreno e y è la corrispondente deformazione trasversale del palo. In generale ad ogni nodo della discretizzazione corrispondono parametri caratteristici differenti della curva p-y o addirittura curve di differente tipo nel caso di terreni di diversa natura attraversati dallo stesso palo.
Le curve p-y possono essere di tipo semi-empirico e danno risultati molto aderenti al reale comportamento solo in presenza dello stesso tipo di terreno e di tecnologia di costruzione del palo in base ai quali sono state dedotte.
In programma vengono assunte (sia per terreno coesivo che incoerente) curve p-y curve di tipo iperbolico (Carter 1984) definite dalla seguente legge costitutiva utilizzabile sia per terreni coesivi che per terreni incoerenti:
u = P/Ks [ Pu / (Pu – P ) ] n
in cui:
u = spostamento
P = pressione terreno in corrispondenza di u
Pu = pressione ultima terreno
Ks = coeff. di Winkler per piccole deformazioni (iniziali) del terreno
n = esponente che controlla l’estensione della non linearità. Si assume il valore di 1 per terreni coesivi e 0,25 per terreni incoerenti.
Questo tipo di legame costitutivo ha sempre fornito, nei controlli sperimentali effettuati, un’accettabile approssimazione in assenza di specifiche curve p-y per il particolare terreno incontrato.
Si sottolinea l’importanza della stima del valore ultimo Pu della pressione resistente del terreno ai fini di una realistica valutazione del carico limite trasversale del palo.
Nel caso di pali in gruppo con interasse minore di 6 volte il diametro dei pali, la stima gli effetti di gruppo per forze trasversali viene effettuata mediante moltiplicatori (<1) delle curve P-y che tengono conto dell’interazione trasversale dei pali per il cosiddetto effetto ‘shadowing’.
In maniera analoga vengono definite, in ogni nodo di discretizzazione del palo, molle non lineari che rappresentano le reazioni tangenziali assiali del terreno lungo il fusto del palo. Le funzioni di comportamento di tali molle vengono definite curve t-z con t che sta per ‘tau’ = tensioni tangenziali e con z che rappresenta la profondità in cui si valuta tale tensione. Viene utilizzata una curva t-z per terreni coerenti ed una per terreni incoerenti (da Reese – O’Neal) restando affidata all’utente la determinazione del valore ultimo della tensione tangenziale del terreno; quest’ultimo valore è determinante per una corretta stima dei cedimenti assiali. Per la sezione di base del palo (anche di diametro differente da quella del fusto) viene assunta una curva di comportamento della reazione del terreno in funzione della pressione limite del terreno (raccomandazioni FHWA americane). Ai fini di una più realistica valutazione dei cedimenti assiali nelle combinazioni di esercizio SLE si raccomanda di ricorrere al terzo modello di comportamento e cioè al modello iperbolico di Chin (1970).
Pali assialmente non lineari (modello iperbolico di Chin)
Questo modello è particolarmente indicato per il calcolo dei cedimenti nelle combinazioni di esercizio SLE e, nel caso di pali in gruppo, va associato alla messa in conto dell’interazione verticale dei pali.
La legge costitutiva di Chin rappresentata in figura è un’iperbole che rappresenta (per interpolazione) la curva Carichi(Q)-Cedimenti(w) assiali del palo. L’equazione parametrica dell’iperbole di Chin (in figura) é:
Q = w / (m + w·n)
Il significato fisico del parametro m (utilizzato nel programma Fondazioni in ca) è costituito dall’inverso della tangente iniziale dell’iperbole: m = 1/KI
Il significato fisico del parametro n è costituito dall’inverso del carico limite asintotico Qlim: n=1/Qlim

Disponendo di curve carico-cedimento ottenute da prove di carico su pali pilota (o anche sulla base di prove dirette non distruttive) è possibile utilizzare un modello assialmente non lineare basato sulla tecnica dell’interpolazione iperbolica per cui la curva carico-cedimento viene interpolata con l’equazione dell’iperbole nella forma: w/Q = m + n·w.
L’utilizzo di questo modello è quindi particolarmente indicato nel caso in cui si effettuino prove di carico su pali pilota fino a rottura. Le NTC definiscono la rottura assiale di un palo quella corrispondente ad un cedimento w pari al 10% del diametro del palo, per pali fini a 80 cm di diametro e, pari al 5% del diametro per pali di maggiore diametro. Di conseguenza il carico limite da utilizzare per le verifiche di resistenza assiali GEO non è quello prima indicato ma è quello corrispondente al cedimento limite di normativa w:
Qlim* = w / (m + w · n)
Una volta calcolato Qlim* può dedursi la resistenza caratteristica e quella di progetto da impiegare per le verifiche GEO assiali del palo. Ad esempio nel caso della tipologia sopra illustrata il valore asintotico della resistenza limite sarebbe pari a Qlim = 1/ n = 1/1.4025 = 0.7130 MN. Assumendo per w il valore di normativa w =0.1 d = 60 mm il carico limite di normativa da assumere in progetto si riduce a:
Qlim* = 0.642 MN.
Il carico limite caratteristico (con una sola prova diretta) è Qk = 0.642 / 1.4 = 0.4585 = 458.5 kN.
Il carico limite di progetto da inserire nell’Archivio tipologie pali è: Qd = Qk / 1.3 = 0.352 MN = 352 kN (R3=1.3 senza distinzione tra resistenza alla punta e laterale). Nel caso in cui la tipologia in discussione appartenga a pali in gruppo come carico limite di progetto Qd può impiegarsi il suo valore caratteristico Qk.
Anche da prove dirette non distruttive che si spingano a carichi dell’ordine di una volta e mezzo i valori di esercizio, possono ottenersi eccellenti valutazioni sia del carico ultimo assiale (da cui dedurre quello di progetto), sia dei parametri dell’iperbole rappresentativa della curva carichi-cedimenti. I parametri m, n della suddetta iperbole di equazione Q = w/(m+n·w) possono essere calcolati con un apposito programma in cui vengono stimati anche le resistenze caratteristiche e di progetto del palo (anche nel caso di prove di collaudo).
I parametri m e n dell’iperbole vengono calcolati mediante elaborazione statistica e rappresentano i due parametri della retta interpolatrice nel piano w-Q·w di rappresentazione dell’iperbole. Migliore è l’approssimazione di tale retta con i punti misurati maggiore è la vicinanza ad 1 del parametro statistico R² (pari al rapporto tra la devianza di regressione e la devianza totale). Cioè se R² è molto vicino ad 1 la curva carico-cedimento è molto ben approssimata dall’iperbole con parametri m, n.
Una volta conseguiti con prove di carico la serie di valori di Q e w è immediato ottenere i parametri m,n,Qd .
Il carico Qlim assiale di collasso geotecnico (GEO) viene stimato tramite l’eq. dell’iperbole ponendo w pari al cedimento limite di normativa (w = 0.1 · D per pali con D<80 cm e w=0.05 · D per pali con diametro superiore: Qlim = w/(m+n w). Nel caso di prove di carico in cui non si raggiunga il suddetto cedimento minimo di rottura (ad es. prove in corso d’opera o di collaudo) è possibile ricorrere all’estrapolazione dell’iperbole utilizzando solo gli ultimi punti misurati in quanto marcatamente non lineari.
La resistenza di progetto assiale Qd del palo viene infine valutata in base alle relazioni di cui al §6.4.3.1.1 NTC a partire dai carichi ultimi medi e minimo, passando per la resistenza caratteristica e detraendo il peso proprio del palo.
Una volta calcolata la resistenza assiale di progetto del palo ed i parametri m, n dell’iperbole è possibile inserire tali dati nella modalità di calcolo assiale non lineare allo scopo di meglio valutare i cedimenti della palificata anche in presenza di platea elastica collaborante (caso delle fondazioni miste). Oltre agli effetti assiali non lineari è possibile valutare l’incremento dei cedimenti (e delle sollecitazioni) dovuti all’interazione assiale tra i pali in gruppo. Detta interazione viene calcolata sulla base dei coefficienti di influenza di cui si dirà più avanti.
Se in fase di progettazione non fosse possibile effettuare prove di carico dirette è ancora possibile utilizzare (per il calcolo dei cedimenti SLE) questo modello a livello di calcolo preliminare nel seguente modo. Si valuta il carico di collasso assiale Qlim mediante metodi analitici sulla scorta dei parametri geotecnici dell’indagine. Noto Qlim è immediato calcolare il parametro n dell’iperbole: n=1/Qlim. Il parametro m vale quindi: m = (1 – Qlim· n)/ Qlim. Una volta stimati i parametri m, n dell’iperbole il valore della resistenza limite di normativa si ottiene imponendo il cedimento limite di normativa w ottenendo il valore ridotto:
Qlim* = w / (m + w · n)
La resistenza caratteristica assiale si può valutare dividendo la resistenza di collasso per 1.7: Qk = Qlim/1.7. Quindi la resistenza di progetto diventa Qd = Qk / 1.3 – PesoPalo.
Per questa tipologia di palo il calcolo degli spostamenti trasversali è previsto lineare stratificato alla winkler (come nel precedente modello lineare).
Fondazioni in c.a. è un software completo che consente di calcolare qualsiasi struttura di fondazione secondo le NTC.
Fondazioni in c.a. è inoltre in grado di importare file di testo contenenti le combinazioni di carico, calcolate in altri software strutturali, trasmesse dalla sovrastruttura.